시드니랩
[Data Mining] 6. Other Clustering Methods 본문
앞서 배웠던 K-means 나 Dendrogram을 활용한 Clustering 기법들은, 하나의 Data, 즉, point가 반드시 하나의 Cluster에 속해야 한다는 단점이 있다. 하지만 실제 분석시에는, 해당 Data(Point)는 분명 다른 Cluster에 속할 수 있는 확률이 있다. 앞서 배웠던 방법에서는, Data의 관점에서, 나머지 Cluster의 확률들은 무시하고, 가장 높은 확률을 보여주는 Cluster과 일대일 맵핑을 해서 Clustering을 실행한 것이다.
◉ Model - Based Clustering
이번에 소개하는 EM algorithm은, Expectation - Maximization 의 약자이다. 이 알고리즘은 하나의 데이터가 각 클러스터에 속할 확률을 정하는데에 쓰이는 알고리즘이다. 앞서 배운 K-Mean 알고리즘과 같이, 처음에 임의의 확률(초기값)을 정해주고, Iterate 하여 특정한 값으로 수렴하는 확률을 찾아내는것이 핵심이다.
각 Cluster에 속할 확률은 Gaussian distribution 이다. (normal distribution) 또, 확률밀도함수를 이용하여 해당 Data가 각 Cluster에 속할 확률을 나타낸다.

각 클러스터는 고유의 평균과 분산을 갖는다. (μ,σ)
각 점이 Data 라고 하였을때, 노란클러스터에 속할지, 파란 클러스터에 속할지, 각 데이터의 입장에서 실제 클러스터에 속할 확률을 정하는 방법이다.
D1 이 노란 클러스터에 속할 확률을 p1, D2가 노란클러스터에 속할 확률을 p2 라고 하고, p1과 p2를 이용하여 새로운 노란클러스터의 평균 u1을 구하는 프로세스의 반복이다.
◉ Density - Based Clustering
이전에 공부했던 클러스터들은 모두 모양이 구형(Sphere cluster)이었다. Density based clustering 방법으로, irregular 한 모양의 cluster을 다룰 수 있다.
DB SCAN
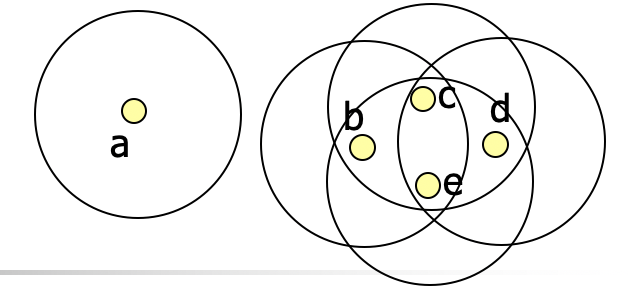
하나의 Data, P 에 대하여, 반지름 ε 를 정의하고, 해당 Data로부터 ε거리 안에 있는모든 점들의 집합을 N(P)라고 하자.
예를 들어 위 경우에는 N(b) = {b,c,e} 이다.
이제 MinPts 를 정한다. 그리고 Minpts 보다 원소의 개수가 큰 N(P)에 대하여, P를 Core point라고 정의한다.
Core Point가 아니지만 Core point를 포함하는 N(P')에 대해서, P' 을 border point라고 정의한다.
border point혹은 core point가 아닌 점들은 모두 Noise point로 정의한다.
예를들어 위의 그림에서 Minpts = 4로 정하면,
N(b) = {b,c,e}
N(a) = {a}
N(c)= {c,b,d,e}
N(d)={c,d,e}
N(e)={b,c,d,e}
따라서 Core point 는 c,e 가 되고,
Border point 는 b,d
Noise point는 a 가된다.
각 Data 들을 core/border/noise 로 분류하고 나서, 아래 Principle에 따라서 Clustering을 실시한다.
1. 각 Cluster은 최소 하나의 core point를 포함한다.
2. 2개의 core point a,b 에 대해서, b∈N(a), a∈N(b) 이면, 클러스터로 정의하고, 그들의 border point 또한 클러스터에 포함시킨다.
3. 모든 noise point는 cluster에 속하지 않는다.
◉ Scalable Clustering Method
새로운 데이터가 추가되었을때, 데이터셋을 잘 다룰 수 있는 것이 Scalable한 Method이다. BIRCH Method를 사용하면, 커다란 데이터셋, 그리고 데이터의 update을 잘 다룰 수 있게된다.
BIRCH : Balanced Iterative Reducing and Clustering using Hierachies
BIRCH 를 떠나서, 각 클러스터들은 다음 3개의 특징을 기본적으로 갖고 간다.
- Mean : 각 클러스터에 속한 데이터들의 평균
- Radius : 클러스터 내, 해당 데이터의 평균에 대한 거리
- Diameter : 한점으로부터 클러스터 내의 특정점 사이의 거리들의 평균

BIRCH 알고리즘은 아래와 같다.

직접 한번 x1,x2,x3,x4 를 찍어보며 코드를 따라가면 쉽게 이해할 수 있다.
하지만 여기서 큰 문제는, Diameter을 계산할때 시간복잡도가 O(n^2)로 성능이 떨어진다.
따라서 BIRCH에서는 radius, diameter, mean 말고 아래 term을 사용한다. 아래 term을 Clustering Feature라고 부른다.
n: Cluster내의 data의 개수
LS : Linear sum of n points
SS : Square sum of n points

구한 n, LS, SS로부터, 시간복잡도 O(1)안에 R 과 D를 뽑아낼수 있다. 따라서 굳이 매번 O(n^2)를 계산할 필요 없이, 빠른 연산이 가능하다.


'랩 > Data Mining' 카테고리의 다른 글
| [Data Mining] 8. Subspace Clustering - Density Based Method (0) | 2020.10.06 |
|---|---|
| [Data Mining] 7. Outlier Analysis (0) | 2020.10.05 |
| [Data Mining] 5. Clustering (0) | 2020.09.23 |
| [Data Mining] 4. FP-Tree (0) | 2020.09.17 |
| [Data Mining] 3. Apriori Algorithm (0) | 2020.09.17 |




