[Cryptography] 14. Secret Sharing - Shamir's Secret Sharing Scheme & Chinese Remainder Theorem

 암호학에서 다루는 한 종류인 Secret Sharing은, 반드시 정해진 인원이 모여야지 비밀을 확인할 수 있도록 설계된 수학 모델이다.

가장 직관적이고 편한 예를 들자면,

 

  "어느 마을에 오형제가 있다. 이 오형제는 아버지가 유산으로 남겨주신 보물을 찾으려고 한다. 하지만 아버지는 보물이 숨겨진 보물지도를 다섯 조각으로 찢어서, 각각 아들들에게 나누어주었다. "

 

위의 예시에서, 아버지의 보물을 찾기위해서 반드시 오형제중 정해진 t명이 모두 모여야지만 보물을 확인할 수 있는 보물지도를 디자인 하는것이 바로 암호학에서 다루는 Secret Sharing 이라고 할 수 있다.

 

✣ 기본 골격

Secret Sharing 의 기본 구조는 다음과 같다.

Secret Sharing 출처 : ResearchGate

 

1. Secret 을 나눠가질 구성원이 n 명이라고 할때, $f_1.....f_n$, 즉 n 개의 함수와 $s'=f(s)$ 인 $s'$을 각각 구성원에게 배부한다. (s는 공유하는 비밀)

2. 구성원 모두가 모여야지만 f의 역원을 활용해서 s를 도출할 수 있도록 설계한다. 

 

각 Secret Sharing 은 어느정도의 인원이 모야이지만 비밀을 알 수 있을지에 대해서 인원수를 정의할 수 있는데, 이러한 Scheme 을 표현하기 위해 (t,n)-Threshold Scheme 이라는 표현을 쓴다. 이때 t 는 Threshold 인원수, n은 전체 구성원의 수 이다.

✣ Shamir's $(t,n)$ Secret Sharing Scheme

 이스라엘 수학자 Adi Shamir 은 RSA를 설계한 인물이기도 하다. 이 Shamir 가 1979년 논문(( How to share a secret", Communications of the ACM, 22 )) 으로 제시한 이론이며, 가장 대중화 되어있는 Secret Sharing Scheme 이다.

 이 Shamir's Secret Sharing Theme 은 굉장히 강력하며, 이론적으로 Secure 하다고 알려져있다.

 

 

1. Secret Distribution

우선, Secret을 배부해줄 딜러를 선정한다. 

Public Parameter :

- p : n+1 < p 인 소수 p

- $x_1 ...... x_n$ : n 개의 값을 $Z_p$ 에서 고른다. 그리고 각각의 x들을 n 명에게 배부한다. $Z_p$ : p-1 이하의 자연수

- $a_1.........a_(t-1)$ : t-1 개의 값을 $Z_p$ 에서 고른다. 이 값들은 딜러만이 알고 있는다. 

 

[Secret Sharing Function] :

Secret Sharing Function 

 

 위 식에서, $y_i=a(x_i)$ 인 $y_i$ 값들을 대응하는 각각 n 명에게 배부한다.

 

이때 딜러가 선택한 $x_i$ 가 0 이면 어떻게 될까? 

=> 당연히 안된다. 그렇게 되면 0 을받은 i 번째 사람은, 비밀 s 를 p 로나눈 나머지를 알게 되므로, 노가다로 s 를 쉽게 얻을 수 있다. 그래서 0 이아닌 $x_i$ 를 배부해야한다.

 

2. Secret working 

 

 배부후에,  구성원 n 명은 모두 각각 해당하는 $x_i$ 와 $y_i$ 를 받게 되었다. 

명심할 것은 반드시 딜러 만이 함수의 계수($a_i$) 들을 알고있다는 것이다.

 

 이제 비밀을 풀기 위해서 구성원 중 t 명이 모였다고 가정하자. 

 

각각 구성원이 가지고 있는 x 값으로 아래 행렬을 만들 수 있고, 이런 행렬을 방데르몽드 행렬 이라고 하며, 역행렬이 존재하는 행렬이다.

Vandermonde 행렬

위 방데르몽드 행렬을 만들고, 아래 방정식을 세우면 이제 비밀 s를 풀수 있는 기미가 보이기 시작한다.

Shamir's Secret Sharing Scheme

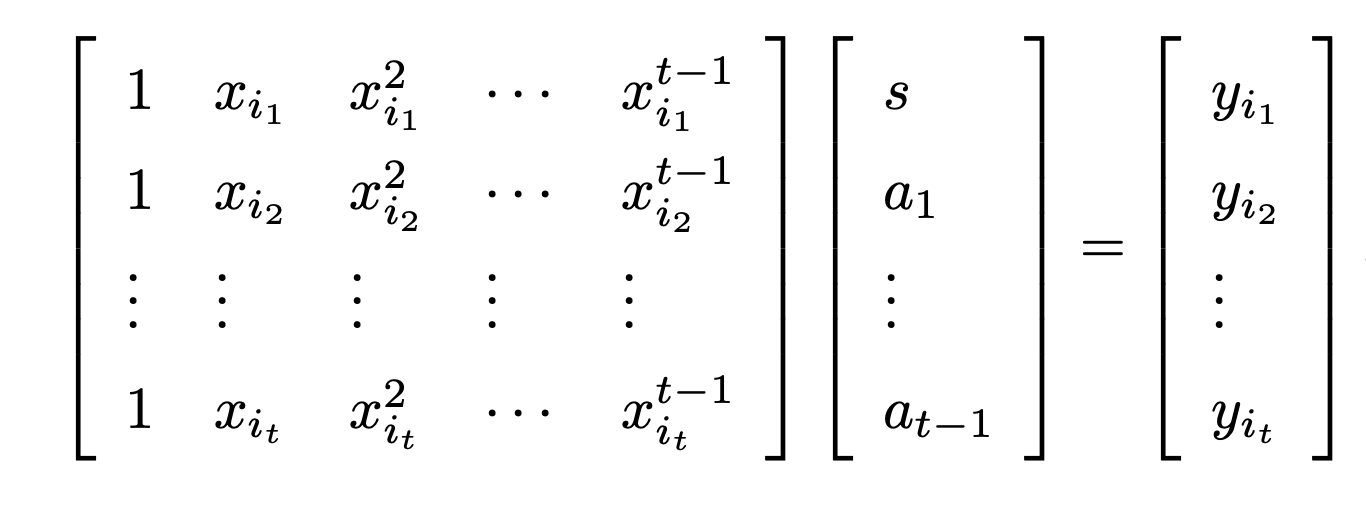
 방데르몽드 행렬의 역행렬을 양변에 곱하면, 주어진 방정식을 풀이함으로써  s를 구할 수 있다

 

 

3. Secret sharing prohibition

 

그렇다면 t-1 명이 모였을때, s를 구할 수 없음을 보여보자. 

마찬가지로 아래 행렬을 만들어서 상황을 표현할수있다.

Shamir's Secret Sharing scheme -2 

 

참고로 위 행렬은 정사각 행렬이 아니기때문에 역행렬을 구할 수없고 따라서 방데르몽드 행렬이 아니다. 

그러면 식을 조작해서 우변을 방데르 몽드행렬의 형태로 만들어서 해결해보자.

 

Shamir's SecretSharning -3

 

방데르몽드행렬 -2

 

Shamir's secret sharing scheme- 3

 

B의 역행렬을 양변에 곱하면 연립방정식을 도출할 수 있다. 

하지만 여기서 우리가 구해야하는것은 s다. 

모든 a의 값들이 0 이 아니기때문에, s 값에 따라 a값들이 변한다는 것을 알 수 있다. 따라서, 여기서는 s 를 구할수가없다. 

 

이렇게 Shamir's Secret Sharing Scheme 의 동작을 확인할 수 있다. 

반드시 정해진 t 명이상이 모여야지만 비밀 s를 확인할 수 있었다. 

 

✡︎ 추가 

 앞서 Shamir's Secret sharing function 을 다시 상기해보면, s가 상수항으로 있는것을 알 수 있다.

Secret Sharing Function 

꼭 상수항에 s 가 있어야만 할까? s 가 굳이 어느 계수로 있던지 상관 없는것 아닌가?

 

=> 정답은, s는 상수항 혹은 최고차 항의 계수로만 존재할 수 있다. 

 

우선, 위에서 B 행렬로 보였듯이, t-1 명이 모였을때 s 를 구할 수 없어야 한다.

 

[s 가 일반항의 계수로 있을때]

s 가 일반항의 계수

[s가 최고차항의 계수로 있을때]

 

 

 

✣  [참고] Chinese Remainer Theorem 

중국인의 나머지 정리로도 (n,n) - Secret Sharing 을 해볼수가 있다. 

 

중국인의 나머지정리 (CRT) : 3으로 나누었을때 2가 남고, 5로 나누었을때 3이 남고, 7 로나누었을때 2 가 남는 수는? 

 

이 정리를 활용해서 구성원 각각에게 숫자 n 과 비밀 s를 n 으로 나눈 나머지 r, 즉 (n,r) 을 나누어 준다. 

 

아이디어에 따르면, 모든 구성원들이 모였을때, 중국인의 나머지 정리를 통해서 s를 복원할 수 있다는 것이다.

 

참고로 중국인의 나머지 정리는 위의 예시에서는

 

x= mod5 part + mod7 part + mod3 part  로 나누어서 계산할 수 있다.

 

하지만 n명이 굳이 모두 모이지 않더라도 나머지를 이용한 힌트를 얻을 수 있기때문에, 완벽하지 않은 Secret Sharing 이다.